Understanding Foucault
A Primer for Beginners
Second Edition By David Anthony HarbourJuly 2001

For those of you contemplating making your own mirror, David Harbour offers a new, easy to understand explanation of the most capable testing method for monitoring the developing figure on your mirror - the Foucault Test. Included are new concept illustrations that are sure to help you thoroughly and quickly master the basics of the Foucault test.
Introduction
A delightful experience with rare flavor awaits one who beholds a celestial wonder with a mirror crafted with his or her hands. Most persons making their first telescope mirror also find another kind of rare flavor in the experience: the reward of meeting a challenge that requires discipline and concentration of one's mental faculties.
Almost certainly the last phase of mirror making, where one imparts the final, precisely defined curve to the mirror's reflective surface, is the most challenging. This final stage of mirror making is known as figuring, inasmuch as it is a process of altering the mirror's curve, or figure into the one required for proper function. The process of figuring is essentially a process of selectively removing very minute amounts of glass in the proper places to bring the curve to the required form. In order to guide the process of figuring we need a sensitive test that will accurately show us the mirror's true figure at every stage of the work.
With this treatise, I will show that for the amateur Foucault has altogether more advantages and fewer disadvantages than any other method of testing. The method is extremely versatile and more than adequately precise. Foucault is even adequate enough for the production of a fine primary mirror for the classical Cassegrain reflector. I have written this exposition in a new way in order to make the basic foundation concepts understandable in as intuitive a way as possible, not assuming any previous familiarity on the part of the reader with any of these founding concepts.
For this reason it seems appropriate to insert a necessary note for those experienced and knowledgeable persons who may want to offer comment on this exposition. You will find many illustrations, descriptions, and explanations that will strike you as perhaps incomplete, or not quite precisely literal, or not exhaustive of the subject. I ask all of you to bear in mind that I am trying to educate the beginner, rather than confuse him or her with too much unnecessary information. My goal is to teach first principles first.
Testing in General, Briefly
Monitoring the developing figure of a mirror can be done with a wide variety of methods. All of these methods fall under two basic genera with their several different species: tests done at center of curvature, and tests done at focus. We consider testing at conjugate foci as a variation of testing at center of curvature.
Testing at focus is very convenient and is the preferred method for many advanced amateurs. The commercial houses also usually prefer it. For the amateur with limited resources wanting to make only one, or a few mirrors, it is not so suitable as testing at center of curvature. This is because both of the best forms of testing at focus, null testing and interferometry, require auxiliary optics that are either prohibitively expensive, or overly challenging for the beginner to fabricate. Thus, we will conclude that testing at focus is not convenient for the purposes of beginners.
That leaves us with the other genus of testing with its various species: tests done at center of curvature. The best forms of this type of testing fall (at least approximately, if not precisely) under two basic forms: null tests, and non-null, quantitative tests.
Null testing at center of curvature we dismiss as not convenient for the purposes of the beginner for the same reason we dismissed it as a testing method for use at focus: it requires auxiliary optics either expensive or difficult to fabricate. In addition, this form of testing introduces an extra level of opportunity for error -- I will merely cite the tragic case of the Hubble telescope's seriously flawed optics for an example of null testing at center of curvature gone seriously awry, even in the hands of seasoned experts.
At last we come to that other species of tests at center of curvature: non-null, quantitative tests. There are two best, most useful sub-species of this kind of testing: the Gaviola, or so-called "Caustic" test, and lastly, Foucault.
A very "great light" in the optical industry once dismissed, in conversation with me, both Caustic (and Foucault) as "useless". After finally mastering both these forms of testing, I understood why he'd made this remark: he used interferometry, a far less cognitively challenging method for testing, and did not have an adequate conceptual understanding of the other methods.
Caustic is capable of monitoring the developing curve on a mirror being figured to an extremely high degree of accuracy. This very precise, rigorous form of testing is, however, both time consuming and tedious in its execution. Additionally, the test apparatus is expensive to purchase, or overly challenging for one without machine tools or machining skills to fabricate. So we will pass on Caustic as also not suitable for the beginner's purposes.
We finally come, then, to Foucault. In defense of its merits as weighed against its demerits, I refer the reader again to my general comments in the second paragraph of my introduction. Additionally, I would like to say in praise of Foucault that it is peculiarly "idiot proof" in a way that null testing at center of curvature is not. Again, I cite the near disaster of the Hubble telescope as an example of the kind of error that can happen with null testing at center of curvature. This kind of error can't happen with Foucault; the nature of the test set-up for Foucault prevents it from "telling a lie". Lastly, I want to add that neither machine tools nor machinist's skills are required to construct a very adequate test apparatus for Foucault. Time has tested Foucault- "Nothing tests truth like time". (I will cover testers and their design and construction after teaching testing essentials -- building a tester is easy).
We Need a Mirror
In order to begin learning Foucault, we need a concave mirror. I cover the mechanics of grinding and polishing the preliminary curve onto the glass in another paper -- we are interested here in learning testing so that we can figure the final, correct curve onto the glass to enable it to give sharp images.
We're going to make our mirror in an imaginary way in order to teach you your very first essential foundation lesson for understanding Foucault.
Perhaps some civilization beyond the earth, with an advanced technology, makes mirrors by a method we shall theorize. Maybe the vanished "Krell" civilization on Altair 4 made their mirrors in the way we shall describe. The Krell opticians will demonstrate how they will impress the initial concave curve onto a twelve inch mirror with a very short focal length. For our first lessons in our treatise on Foucault testing, a very short focal length mirror serves for clarity in the illustrations better than a longer focal length mirror. We will pretend that Foucault will serve well for testing such a very short focal length mirror -- even though we know that Foucault is not satisfactory for testing mirrors of extremely short focal length. Remember that our purpose is to teach.
Molding a Mirror
Perhaps archaeologists will discover that the long vanished Krell opticians did not grind their mirrors, but molded them. Let us theorize that they used a large, perfectly spherical ball of their fabulously durable "Krell metal" to impress the initial concave curve onto a mirror being made. We will refer to figure 1 as we discuss this molding technique. Looking at figure 1, we see a depiction of a large sphere, drawn as if it were transparent. A dotted line of longitude, and a similar line of latitude, are drawn onto the surface of the sphere to help convey its three dimensional shape. On the far side of this apparently transparent sphere of Krell metal we can see a telescope mirror pressed up against its smooth, spherical surface.
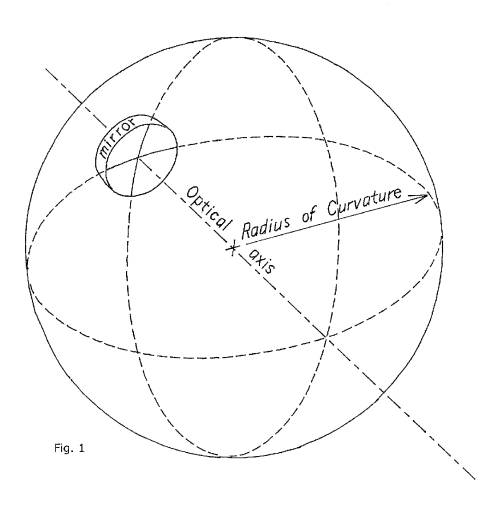
And this is the first step in Krell mirror making: the initial curve is impressed onto the surface of the glass after it is heated to near melting by pressing the mold with the hot glass up against the surface of the big sphere. One can plainly see that the shape of the curve impressed onto the glass with this molding procedure is an exact representation of the shape of that section of the sphere's surface that it was held in contact with.
First Essential Foundation Lesson:
Now this method of molding a mirror helps us understand some things. Firstly, it helps make clear what is meant when we say that this mirror's curve is spherical; of course it is spherical -- words are not really needed to describe its curve -- its shape is a direct impression of the big sphere of Krell metal. So we have a spherical mirror now, which after further work will become a telescope mirror. Let's look at some features of this spherical mirror. We understand now that it has a spherical shape, or figure, after being molded with the big sphere of Krell metal. We will often have occasion to refer to its figure's radius of curvature. Please look at figure 1 again; it is immediately apparent from figure 1 what we mean by radius of curvature when referring to this mirror's spherical figure; its radius of curvature is identical to the radius of curvature of the surface of the big ball of Krell metal used to mold it with. So our imaginary molding technique for impressing the initial concave curve onto our mirror has taught us two things -- what is meant by the term spherical, as a description of a mirror's figure, and what is meant when we speak of its radius of curvature.
Next Essential Foundation Lesson
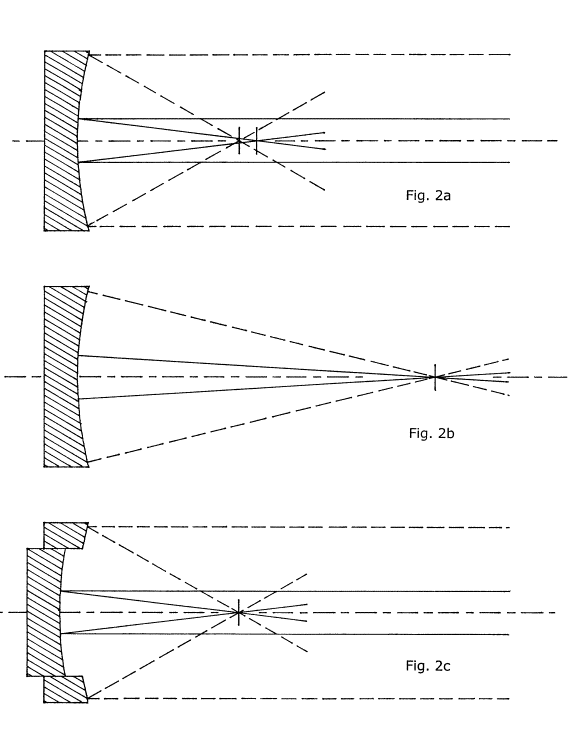
While learning this next lesson, we will be referring to figure 2(a) and figure 2(b). Figure 2(a) shows a view of our newly molded mirror with its concave, spherical figure in cross section, receiving four parallel rays of light as they enter from the right side of the diagram. These rays of light are parallel because they originate from a very small source of light a very great distance away from our mirror -- we will specify that the light source is infinitely far away. The rays of light striking the areas of the mirror's surface near its edge are shown as dashed; the rays of light striking the mirror's surface near its central regions are shown as unbroken. The line shown proceeding through the center of the face of the mirror we shall call its optical axis. Strictly speaking, a spherical mirror does not have an optical axis, but we will pretend that it does, for teaching purposes.
Now, looking at figure 2(a), we can see that the light rays are reflected from the concave spherical surface of our mirror and focused onto a specific region along the mirror's optical axis. A casual glance suggests that the mirror will focus all four light rays down onto the same point lying on the optical axis, but a close inspection will reveal that this is not quite the case. The rays of light that were reflected from the outside regions of the mirror's concave spherical surface (represented by the dashed lines) come to a focus at a point lying on its optical axis slightly closer to the mirror than those rays of light reflected from the interior regions of the mirror's concave spherical surface. In our illustration, two short, vertical lines mark these two different locations along the optical axis. We will think of these two short, vertical lines as representing two different locations of a small square of ground glass, on which to see the focused image of the infinitely distant light source. Or, just as usefully, we might think of them as representing two different locations of a small square of photographic film, with which to record the focused image of the infinitely distant light source. What is essential for us to understand here is that a mirror with a spherical figure (we will call this kind of mirror a "spherical mirror") receiving light from infinity cannot focus all of this light reflected from its inner and outer zones into the same focal plane. This defect is known as spherical aberration (naturally enough).
The mirror in our example as molded by the Krell in their optical plant has a very short focal length; really, its focal length is even too short for us to use it in a telescope. We have made it very short so that the diagrams will be clearer and more instructive. When we speak of a mirror's focal length, we mean, of course, the distance from the mirror's concave, reflective front surface to the point (or, more precisely, a field of all possible points, a "focal plane") into which any given bundle of parallel rays received by the mirror from infinity will be focused. In short, the focal length is the distance from the front surface of the mirror to its image, or focal plane. The diameter of a mirror, divided into its focal length, gives us its focal ratio. We will pretend that our Krell opticians have molded us a 12" mirror with only a 12" focal length. Thus, the focal ratio of our mirror is unity, and expressed (by convention) as f/1.
While we are still considering figure 2(a) it will be helpful, here, to understand that this illustration can be thought of as representing only how a mirror makes an image of a very distant, apparently very small, single light source, such as a single star that the telescope is aimed directly at. A little thought will make it apparent, however, that for an image field comprised of more than a single star, such as for instance a galaxy, a mirror will be receiving many different bundles of parallel light from many different points of origin in its field of view, each of these bundles approaching the mirror at a slightly different angle, with each bundle reflected at a correspondingly slightly different angle from the mirror and focused into separate, disparate points in the focal plane, building up an image all across this plane.

Now, let's look at figure 2(b). For this part of our lesson we have moved the infinitely distant single, small light source up very close to our mirror but still lying on its optical axis. We have brought it up to a point where light rays fanning out from this very minute light source will each strike the mirror at an angle that we will loosely describe as a right angle. After striking the mirror, each will be reflected back at the very same angle, returning exactly along its outgoing path back to its source. For a spherical mirror, there is only one point along its optical axis where the light source can be located for which the mirror will reflect (and focus) its spreading rays exactly back onto it. The location of this point is identical with the mirror's center of its radius of curvature. And now we've learned in detail this new essential foundation lesson: A spherical mirror, receiving a bundle or bundles of light rays from infinity, cannot focus all of the light rays in each bundle into the same image, or focal plane. However, if the light source is located at the center of its radius of curvature, it will precisely focus all the source's light rays back onto its center of curvature. Understanding this feature of the spherical mirror's optical properties will help us later on master necessary concepts for Foucault.
Next Lessons
We will not call this next instruction an "essential foundation lesson", but it will help prepare you for one.
We've seen that a spherical mirror cannot focus light from infinity that has been reflected from different areas of its surface all into one focal plane. This defect is known as spherical aberration and will prevent the mirror from focusing light accurately enough to form a sharp image.
Fixing the Defect
How can we possibly remedy this defect, this inability of a spherical mirror to accurately focus all its reflected light into one focal plane? If we look again at figure 2(a) we can find a clue as to one possible remedy -- since the rays of light that are being focused by the near-central regions of the mirror are coming to a focus farther away from the mirror, why can't we just move the central portion of the mirror back a ways, until its focal plane is congruent (in the same location) as the focal plane for light focused from the outer (near mirror's edge) regions? Figure 2(c) shows how this remedy might work: note how the central portion of the mirror has been parted from an outer annulus, and moved backwards by a distance required to bring its focal plane congruent with that for the outer annulus. The remedy was actually tried by a famous nineteenth century telescope builder, Lord Rosse, whose chief contribution to astronomy was his giant reflector at Birr castle and his discoveries with it. The remedy is impractical for several reasons, however, and probably tried only once. But I have shown you Lord Rosse's experiment for instructional reasons -- we are going to use his curious, once ever two-component mirror to learn an interesting lesson that will help us understand Foucault. Before we meet our "Lord Rosse Special" again, however, we need to learn about the knife-edge.
Leon Foucault
The nineteenth century saw many important foundation developments that contributed to the perfection of the modern reflecting telescope. Leon Foucault (1819-1868) contributed some of the most important of these innovations. In addition to demonstrating the superiority of glass (with silver coating) over speculum metal for mirrors, he presented the world with a powerful method for critically surveying optical surfaces -- the knife-edge. In his hands and the hands of his followers various developments and applications of the use of the knife-edge as an adjunct for accurately figuring optical surfaces were developed over time.
The Knife Edge
Let's look now at figure 3a. We have our 12" spherical mirror, molded for us by the Krell opticians, standing on edge. We've left the two meridians of longitude and latitude, impressed onto the mirror's front surface from the big ball of Krell metal, to remind us of the mirror's concave shape.
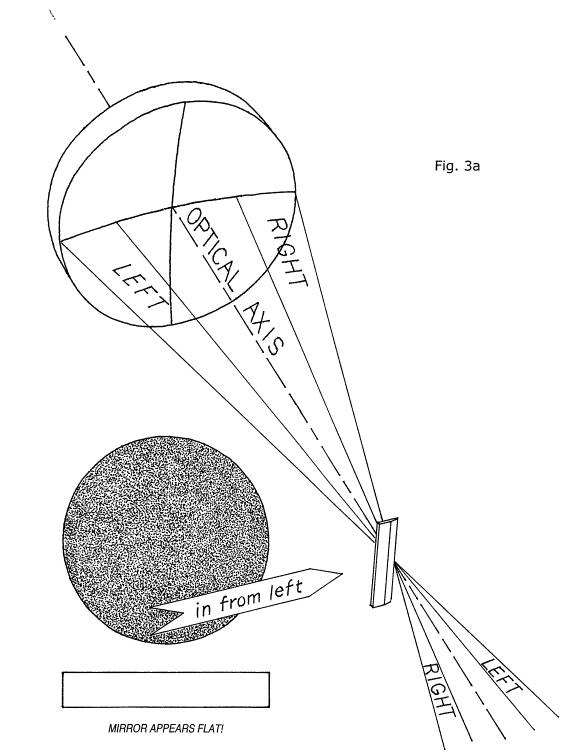
Four rays of light are depicted as being focused by our mirror down to a point, apparently just adjacent to the edge of a small razor blade standing on its end. Please note that the edge of the blade is extremely close to the mirror's optical axis. These light rays have emanated from a very tiny light source located on our mirror's optical axis at the center of its radius of curvature and fanned out to its concave surface, to be reflected back along their outgoing paths to converge right back onto their tiny light source.
After converging onto their original source, they continue on, fanning out and away. Although we show only four light rays fanning out from this tiny bulb, in order to keep the diagram uncluttered, we will keep in mind that in reality there are light rays fanning out from this little light source in great numbers in every direction and are striking the mirror's front surface all over.
In this illustration our tiny light bulb at center of curvature and the razor blade's edge are virtually in the same location. In order to keep the illustrations as uncluttered as possible, we will adopt the convention of not showing this light source at center of curvature.
The mirror is actually forming an image of our tiny light source right at center of curvature, and even if we do not have a piece of ground glass or film in place here for the image to be focused on, it will still be in place here, just suspended in the air -- a so-called "aerial image".
Now we are going to do an experiment. First, we will move the razor blade away from the optical axis to the left, slightly -- just enough so that we are sure it is not obstructing any of the reflected rays of light crossing over the optical axis here at center of curvature (we will shorten "center of curvature" to "C of C" from here on out). Next, one of us places his or her eye in position on the mirror's optical axis just behind and very close to the tiny aerial image formed there at C of C. Now, with one's eye placed very close to this tiny image, one's eye will not be able to focus on it and see it, but rather, one will see the mirror beyond it. The mirror will appear brightly and evenly illuminated all over, because it is reflecting the light from the tiny light source equally from every portion of its surface.
Next, we begin to bring the razor blade in from the left, very slowly, until its edge begins to obstruct, or occult part of this light returning from the mirror. Now, inasmuch as each and every part of the tiny image of the light bulb is receiving a bundle of light originating from the mirror's entire surface, when the razor blade begins to obstruct it, the light in each of these bundles from the mirror is reduced equally and simultaneously from every part of the mirror's surface, and the mirror begins to darken all over simultaneously and equally, "graying out" all over, uniformly. We may halt the advance of the knife-edge (KE) when it is obstructing about half of the returning light from the mirror; or, we may continue its advance until the returning light is entirely cut off. If our mirror is accurately spherical, and the KE approaches and crosses the optical axis at exactly the C of C, the mirror will darken, or null, simultaneously, all over its surface. When we use the KE to examine our spherical mirror from the vantage point of its C of C this way, the mirror will appear perfectly flat. We know for certain that it is spherically concave, but nevertheless it appears flat when viewed this way. And as it turns out, there are important advantages for us in pretending, or imagining the mirror as flat, instead of concave. And this is the essence of another essential foundation lesson: we will adopt the convention of always visualizing the mirror's surface as flat, and any deviations from this imaginary flat figure will always be visualized and depicted as such.
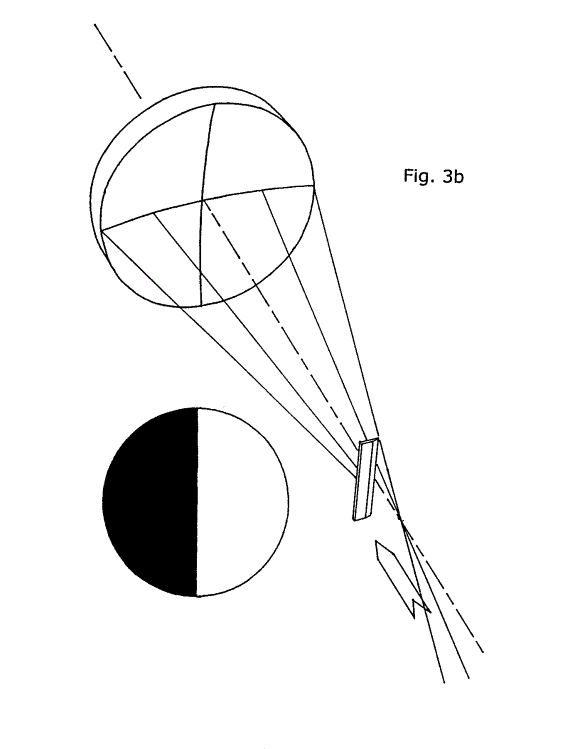
Now, let us consider figure 3b. Our razor blade (KE) can be moved at right angles to the mirror's optical axis, and also parallel to its optical axis, toward or away from the mirror. In figure 3(b) we have moved it a little ways toward the mirror, leaving its edge just adjacent the optical axis. The KE is now blocking only those rays of light coming from the left side of the mirror, and only its left side appears dark. If we withdraw the KE to the left, away from the optical axis, this dark shadow on the left side of the mirror will recede to the left, also. If we advance the KE back in again to the optical axis, the shadow will reappear and advance in the same direction across the mirror's surface. If we continue advancing the KE all the way across the optical axis (OA) until all of the returning rays of light are blocked, the entire mirror will go dark as the KE's shadow advances all the way across the mirror from left to right.
Now, let's back the KE away from the mirror along its OA, passing through C of C until we are beyond it by about the same distance as we were just previously inside it (closer to the mirror than C of C) as shown in figure 3(c).
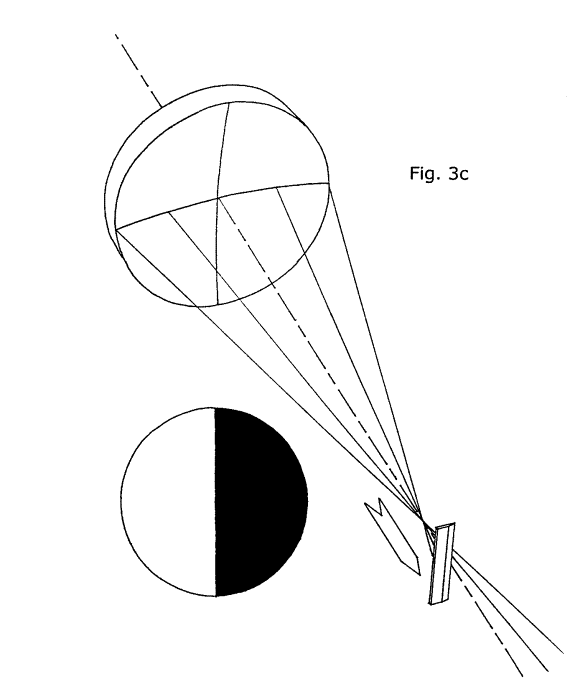
Suddenly, even though we have not moved the KE laterally, the right half of the mirror now appears darkened! Look at the illustration carefully: with the KE beyond C of C, it is now blocking the rays of light from the right half of the mirror after they've crossed the OA. The light rays from the left half of the mirror, however, have crossed over the OA in the other direction, away from the KE, and are not obstructed by it at all. Now, if we back the KE out to the left again, away from the optical axis, the shadow on the right side of the mirror will advance in the opposite direction of the KE, towards the right. If we back the KE out all the way to the left, so that it no longer obstructs any of the returning rays from the right half of the mirror, the mirror will again appear bright all over. Alternatively, if we advance the KE back in again from the left until all of the rays of light returning from the mirror are obstructed (occulted) then the mirror will go dark all over as the KE's shadow advances in from the right, again moving in the opposite direction as the KE.
We've just made a wonderful discovery, and learned our next, essential foundation lesson: the KE can tell us whether we are inside of, outside of, or exactly at the center of curvature of a spherical mirror.
The "Lord Rosse Special"
We've learned that the knife-edge can tell us just about one important thing about a perfectly spherical mirror: where its center of curvature is. And although spherical concave mirrors have their places in astronomical optics, we are primarily going to concern ourselves with another species of concave curve that is not as simple as the sphere. Remember -- a spherical mirror suffers from spherical aberration - a characteristic that prevents it from accurately focusing light from infinity, preventing it from forming sharp images.
Remember our discussion about Lord Rosse's efforts to cure spherical aberration with his curious two-component mirror? We're going to use his novel mirror to learn a new, essential foundation lesson.
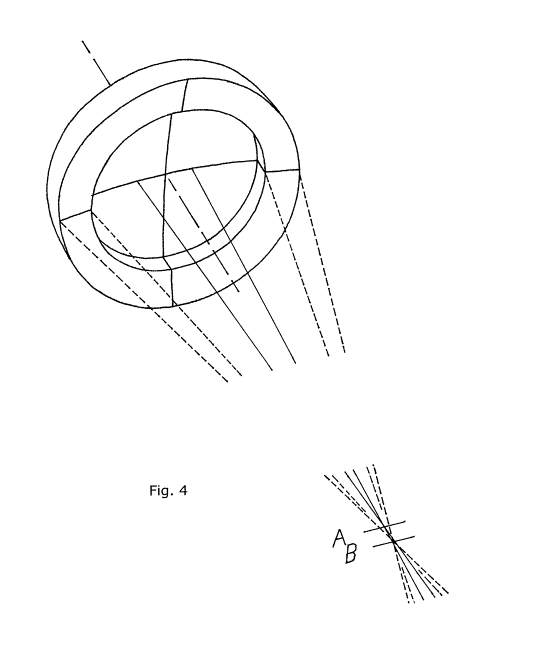
Let's take a look at figure 4. It shows us Lord Rosse's two-component mirror standing on edge. We've put two meridians across its front surface to help us visualize its shape. This mirror was made by parting a single, one piece spherical mirror into two components. Before it was parted and the two components relocated slightly with respect to each other, it had, of course, a single radius of curvature and therefore a single center of curvature. But now this "compound" mirror has two different centers of curvature. They are marked in the diagram as two short lines lying across the optical axis in slightly different locations, at "A" and "B". Two unbroken lines representing two rays of light are shown emanating from the C of C marked "A" and fanning out, striking the interior of the central component of the mirror. After being reflected from this area, they converge back on their C of C, crossing the OA at that location and then fanning out beyond. Four dashed lines, rays of light, are similarly shown fanning out and striking the outside component or annulus of the mirror and then being reflected back to their C of C, crossing the optical axis there and fanning out beyond. Let's take a close-up look at this region of the OA where all of these rays are crossing it.
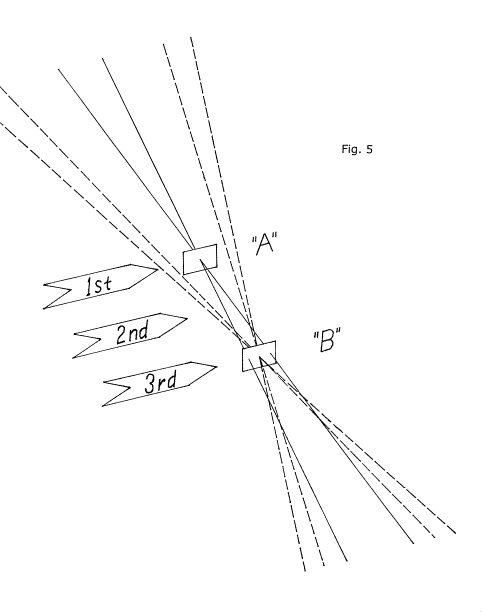
In figure 5 we've zoomed in close to see what's happening more clearly where these light rays are crossing the OA. At each center of curvature for each component of the mirror we've positioned a little square of ground glass (or we may think of it as a little square of film) to represent each component's center of curvature. We have located three "arrows", labeled 1st, 2nd, and 3rd for three positions along the optical axis. We're going to explore the optical axis in this region with the KE, and inspect the mirror with it positioned, in turn, from each of these locations represented by the little arrows. We show these locations identified by arrows to remind us that in each location we will bring the KE in from the left, starting with it well clear of any returning light rays from the mirror, so that we may observe the order of progression of the unfolding appearances as the KE is moved inwards. We will omit any depiction of our "imaginary" light source at each center of curvature to keep the drawing uncluttered. And this time we will not show the knife edge, either, leaving you to imagine it and its action as it moves inwards from each of these locations in turn.
Let's start with the KE in the position marked 1st, the position closest to the mirror, and work successively outwards to the other locations, in turn.
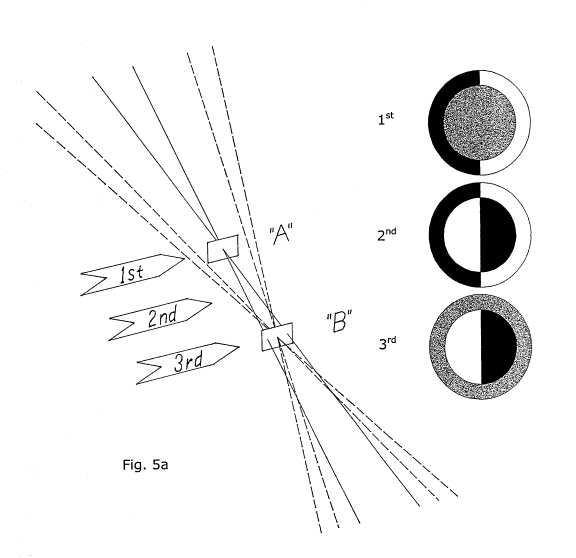
As we begin moving the KE in from the left, it first encounters light rays returning from the left half of the outside annulus of the mirror, obstructing its left-most rays first. As the KE continues slowly advancing inwards, more and more light from the annulus is obstructed, progressively from left to right, and we see a very dark shadow proceeding inwards across the annulus from left to right. The shadow, so far, is moving in the same direction as the KE. By the time the KE is nearly just adjacent the optical axis, the left half of the mirror's outside annulus is almost completely filled in with dark shadow. Finally, as the KE moves the very last, tiny increment of distance to bring its edge just to the OA, it begins to partially and simultaneously obstruct light from every part of the central component of the mirror here where it crosses the optical axis. As the KE obstructs this light, the central component grays out, or "nulls". We have detected the central component's center of curvature with the KE. Halting the KE's advance now, we note the mirror's overall appearance, and it appears as in fig. 5(a), with the left half of the outside annulus completely dark, its returning light completely obstructed by the KE. The central region is nulled, with its light only about fifty percent obstructed. The right half of the outer annulus is still completely bright, as all of its rays pass well clear of the KE's edge, not at all obstructed in the least.

After taking careful note of the mirror's appearance with the KE in its last position at the arrow marked 1st, we next withdraw it laterally, away from the OA until no light from the mirror is obstructed, and then back it away from the mirror until it is at the arrow marked 2nd, midway between the centers of curvature of both the mirror's components. With one's eye again in place on the optical axis looking at the mirror, the KE is again brought very slowly in from the left until it begins to obstruct the leftmost rays of light returning from the mirror. As in the 1st position, the leftmost regions of the outside annulus begin to darken first as we see the KE's shadow again move in from the left, in the same direction as the motion of the advancing KE. Continuing the slow, rightward motion of the KE, we begin to get close to the OA and the left-hand side of the outside annulus becomes nearly filled with dark shadow as before when we were working at the 1st position closer to the mirror. But then, a curious thing begins to happen: as the KE continues its slow advance up to the OA a dark shadow begins to move in from the right, travelling leftwards across the right half of the central component of the mirror. The rightmost regions of this component begin to darken as the KE obstructs their reflected light on the left side of the OA where they've crossed over a little ways after having passed through C of C for this central component of the mirror. Continuing the KE's advance right up to the edge of the OA we observe this shadow continue and complete its advance inwards from the right hand side of the central component until the entire right half of this component is in dark shadow. After stopping the KE's advance right at the OA, we note the overall appearance of the mirror. The light from the left half of the outside annulus is completely blocked, and the light from the right half of the inside component is completely blocked, and bothof these areas appear very dark. However, the returning light from the right half of the outside annulus passes well clear of the KE and it remains brightly illuminated. In addition, the light from the left half of the inside component passes well clear of the KE and this area also remains fully illuminated. The overall appearance of the mirror is as in fig. 5a, "2nd".

We will finally relocate the KE in the 3rd position, starting again with it well clear of all returning light rays and then advancing it in towards the OA from the left. As it advances in from the left, the first light it encounters and obstructs is that returning from the right half of the inside component of the mirror. This light has already crossed over the OA and is well clear of it to the left in this 3rd position. As the KE continues its inward advance towards the OA, the edge of the dark shadow advancing in across the right half of the central component moves leftwards, in the opposite direction of the KE's motion until the right half of the inside component is nearly all dark. Then, as the KE advances the last small increment of distance up to the OA, it begins to obstruct the returning light rays from every portion of the outside annulus' surface equally and simultaneously, causing this central area to gray out, or null all over simultaneously. The KE has detected the C of C for this outside annulus of the mirror. We halt the KE's advance here, right at the optical axis, and survey the mirror, noting its appearance, as in fig. 5(a), "3rd". The right half of the inside component is completely dark, all its returning light occulted, and the left half is completely bright, none of its returning light occulted. The outside annulus is evenly nulled, as our KE is precisely at its center of curvature.

Exploring the optical axis of our "Lord Rosse Special" with the knife-edge has been our first experience in surveying the surface of a concave mirror whose figure is something other than a simple sphere. We've garnered many different lessons with this exercise that will now be well understood intuitively, without further necessity to elaborate verbally. One, however, needs to be gotten in mind in a very unequivocal fashion, and so we now state it here as an essential foundation lesson: The appearance of any concave mirror when surveyed with the knife edge will always be different when viewed from different locations for the knife edge along the optical axis.
Correcting Spherical Aberration
Before leaving our "Lord Rosse Special" it will be instructive to understand why it didn't work so well as a remedy for spherical aberration.
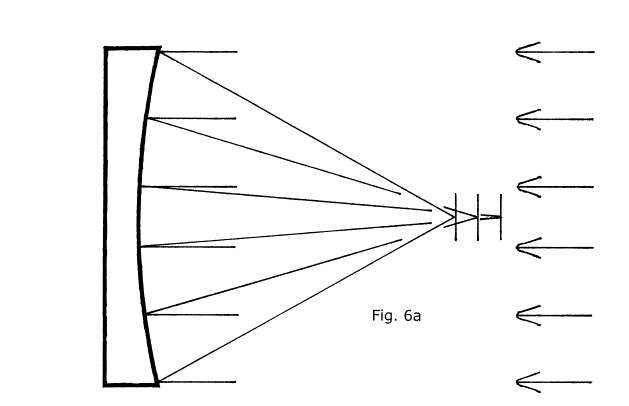
In figure 6(a) we show a very short focus mirror in cross section receiving light rays from infinity and focusing them along a short region of its OA, as in our earlier diagram, fig. 2(a). In that previous diagram we showed light rays from infinity striking the mirror near its edge and near its center and being reflected onto a short region of the OA. For fig. 6(a), however, we show some rays in addition to those for the central and near edge regions. These rays are striking the mirror's face in a zone intermediate between its edge and center regions. The illustration makes it plain that the spherical mirror cannot focus rays of light reflected from any of these zones into the same focal plane. Three short lines lying across the OA represent the three different focal planes for light reflected from these three zones or areas of the mirror.
Contemplating this diagram should lead one to an intuitive insight: for as many zones as we care to demarcate the mirror's concave surface into there will be as many disparate focal planes for. It should now be clear why a two component "Lord Rosse Special" will not work well; it is optimized for only two zones for the entire mirror: a narrow zone near the edge, and a small region very near the center. All other zones for either component of the two component special will still have widely disparate focal planes.
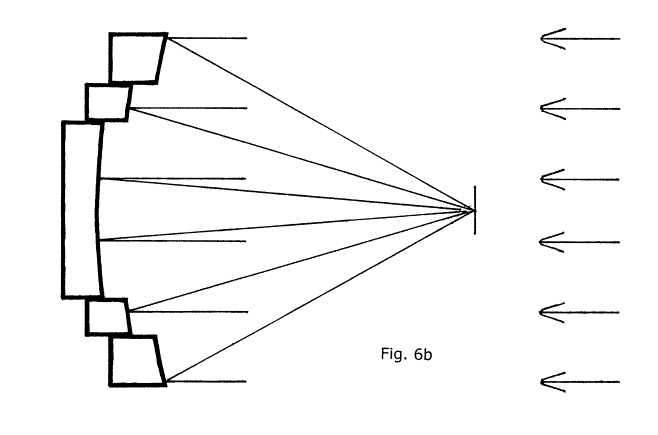
fig. 6(b) shows a hypothetical three component mirror in cross section. We might reasonably expect this three component mirror to work better than a two component one, focusing reflected light from the zone intermediate between its edge and center into a focal plane more congruent with those for focused light from the other zones. But a little thought here will reveal the impossibility of such an approach: each of the three new components is still a section of a sphere, and therefore will each have disparate focal planes for its different zones. In order to optimize the correction to bring the many disparate focal planes congruent, we would have to go on "surgically" subdividing the mirror further and further into more and more nested components, annuli, offsetting each one by the required amount from its neighbor along the OA.
As a conceptual exercise, however, Lord Rosse's approach points the way to a more practical solution: we can offset the successively more central regions of the mirror, successively, from the successively nearer edge regions (relative to a sphere) simply by excavating these successively nearer central regions more deeply. We will then no longer have a concave surface representing a revolution of a circle (a sphere) but some other species of figure of revolution. And this is in essence the time-tested method for altering a spherical mirror's figure into one for which all zones of its concave surface have congruent focal planes, i.e., one that will focus light from its entire surface into the same focal plane. The particular species of surface of revolution that can do this is a curve that geometers long ago designated as one of a family of specifically defined sections of a cone: the paraboloid. And now we are well enough prepared with previously learned founding concepts to introduce the next very important essential foundation lesson: the properties of the sphere and the paraboloid are exactly reversed with respect to each other with regards to each's conjugate focal planes. The sphere, while unable to focus light from infinity into one focal plane, will exactly focus all light received from its center of radius of curvature into one focal plane. Alternatively, the paraboloid, while unable to focus all light from its center of curvature into one focal plane, will exactly focus all light received from infinity into one focal plane. Strictly speaking, a paraboloid does not have a center of radius of curvature, since it is not a sphere; but we will take liberty and use language loosely here in order to help illustrate a concept.
This curious order of features of the curves of conic sections seems almost to have been by design for those of us who want a convenient and quantitatively precise test procedure for monitoring the development of the paraboloid during figuring. In particular, we are happy that the paraboloid cannot return light from a source located at its approximate center of curvature into one focal plane, but instead returns it into different focal planes strung out along its optical axis.
Summary, in Graphic
We're ready to learn the actual test procedure now. Since the essence of the test is embodied in our last essential foundation lesson, we will briefly recap this lesson in a compact, graphical form, so that you will get it firmly in mind. Let's look at figure 7.
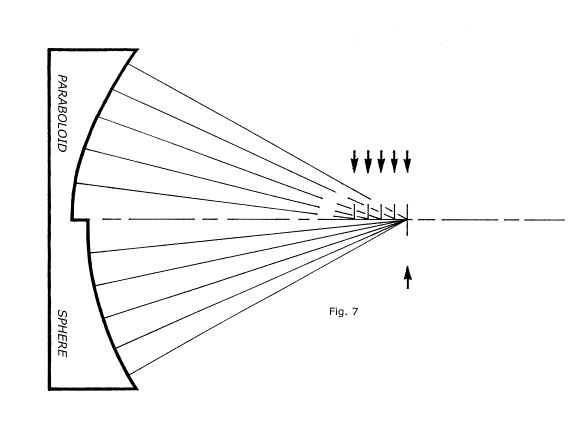
We show yet another, curious, hypothetical mirror in cross section here. This imaginary mirror is divided into two different regions: the bottom half has been left spherical, but the top half has been figured paraboloidal. On the optical axis (out to the right) we've located the center of curvature of the lower, spherical half of the mirror. Light rays are fanning out from this C of C, striking the mirror, and returning back to its C of C. The little arrow below the optical axis marks the C of C.
Now, the upper half of this mirror is paraboloidal. We may reference it with the lower, spherical half of the mirror by specifying that it's very edge zone or region is congruent with the sphere represented by its lower half. This illustration makes clear, at a glance, what we used words to describe as our last essential foundation lesson: the sphere can return all light originating at its C of C precisely back to that C of C; the paraboloid cannot. For this paraboloidal part of the mirror, we show light rays emanating from the C of C of the lower, spherical part its edge is congruent with. Note that it can return only light from this edge zone back to the sphere's C of C. All regions, zone wise successively closer to the center of this paraboloid, will return light to focal planes that are successively closer to the mirror. The five different arrows pointing downwards indicate the five different focal planes for light reflected from the five different zones on the paraboloid (the same zones, radius wise, as for the sphere). All that remains is to show you that the disparity between these various focal planes for the paraboloid can be specified for the figure we desire, and that they can be commanded into their desired locations along the OA by figuring the mirror.
Now, although not critically necessary, it will be useful to understand an interesting lesson here before we begin testing.
In the course of testing their mirrors, experienced users of Foucault more or less pretend, when observing the knife-edge null a narrow zone on the mirror, that they have detected this narrow zone's radius of curvature. It should now be clear to all, however, that this notion can only be a useful fiction for the mirror maker. No zone located on a paraboloid, however narrow, is spherical, and therefore cannot have a center of curvature. But since a very narrow zone can return most of its light to a relatively precisely detectable center on the OA, we tend to think of it as in some way approximately spherical.
Test Apparatus
We will cover tester theory, design, and construction exhaustively in another treatise. Our purpose here is to learn the test procedure, so we will limit our discussion of tester features to essentials. Our test apparatus is comprised of two basic functional components: (1) A mounting platform stage providing linear, translational motion in X and Y axes; and: (2) A very minute light source and knife-edge carried on this stage in a plane perpendicular to our mirror's optical axis.
The knife-edge and the light source are both mounted congruently in a plane (mounted in the same plane) through which the mirror's OA passes perpendicularly. This assembly is in turn mounted on the moveable platform stage so that it can be moved at right angles to and also along (parallel to) the mirror's OA. A dial or screw micrometer is provided for reading the amount of travel of the Y movement stage (motion along or parallel to the OA). Inasmuch as our light source and knife-edge are both mounted on the same plate carried on the platform stage, they move together as a unit in both X and Y axes. Special note: most experienced workers are more familiar with testers having a stationary light source, with only the KE moveable. In our treatise on testers, we will show why carrying both KE and light source together is more advantageous.

Surveying and Measuring the Paraboloid
Figure 8a through 8f shows the appearance of a fully parabolized short focal length mirror for six different positions along its OA as viewed with the KE. By convention we will always begin by pre-setting the micrometer for our tester's Y-axis movement at zero, and locating the tester to null the central region of the mirror. From there we will work the KE backwards along the OA away from the mirror, to find the null point, successively, for several different designated zones on the mirror. Below each depiction of the mirror's appearance ("apparition") for each setting of the KE, we show a drawing depicting the mirror's apparent cross-section. Remember, we said we would always think of a concave spherical mirror as flat when viewed as nulled from its center of curvature. Similarly, we will think of the shape of the paraboloid when viewed with the KE as a variation from the flatness of our "flat" reference sphere.
After nulling the very central region of the mirror, we advance the KE away from the mirror and stop at the location shown at fig. 8b. Note that the mirror appears to have an annular, circular "crest" surmounting an apparent, gentle bulge all around its center just a little ways out. Our KE is exactly at the C of C of a very narrow zone surmounting this crest. More accurately (as no zone on a paraboloid can truly have a center of curvature) we are at that point on the OA where that zone's rays are exactly crossing it. Our micrometer will show us, when we inspect it, how far the KE moved backwards to provide this particular apparition of the mirror. The micrometer indicator will show us the KE's location along the OA where this zone's light rays cross over it, relative to its previous location.

We may continue backing the KE away from the mirror, noting, in succession, the other apparitions at c,d,e, and f. The micrometer will always show us the relative location along the OA for the C of C of the narrow zone represented by the crest of the bulge. In addition to being able to locate the C of C for any zone being nulled by our tester fairly precisely along the OA, we can also measure the location of the zone itself on the mirror, its radius from the center of the mirror. And these are the only two quantities we need to determine accurately during the figuring of our mirror in order to shape it into a section of the true paraboloid.
We will pre-determine which zones' centers of curvature we want to monitor before we begin figuring. Conventions or rules about the number and locations of zones for testing vary with workers. The popular convention of dividing the mirror into zones of equal area probably is most advantageous. Zones of equal area will provide for increasingly narrower and more closely bunched zones, successively, outwards towards the mirror's edge. This seems reasonable in that we must figure the outer zones to tighter tolerances than the inner zones. It is very much true, as an older master once told me, that: "The edge zone sets the mirror's performance."
Let us take for an example a project to figure a ten inch mirror of sixty inches focal length. To find the location of the middle of each zone (as a radius from the center of the mirror) for any diameter mirror, multiply the mirror's radius (in this case, 5 inches) successively by: 0.316; 0.548; 0.707; 0.837; and 0.945. For our ten inch mirror the middle of each zone computed in this way will, be, successively: 1.58"; 2.74"; 3.53"; 4.185"; and 4.725" as measured from the mirror's center (i.e., as radii).
For the mirror's curve to be the correct section of a true paraboloid for its given diameter and focal length, the C of C of each zone is fixed by formula. The location of each zone's C of C is farther away from the C of C of the very central region of the mirror by the following distances:
- Zone 1 (1.58"r): 0.01"
- Zone 2 (2.74"r): 0.031"
- Zone 3 (3.53"r): 0.052"
- Zone 4 (4.185"r): 0.073"
- Zone 5 (4.725"r): 0.093"
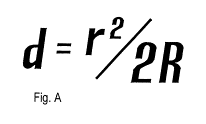
These values are determined by formula (fig. A) where "r" represents the radius of a zone on the mirror and "R" represents the radius of curvature of the mirror (as imagined, of course, as spherical, before figuring). This is not quite the formula most experienced workers are familiar with, as more commonly their testers have their light source fixed and only move the knife edge along the mirror's OA. As we explained previously, we will carry both the KE and the light source on a small plate together in order that we may move them simultaneously along the OA.
It is singular and curious how some obsolete practices continue to be popular very long after much improved ones have been demonstrated. In our article on tester design and construction, we will show several enormous advantages for carrying both KE and light source together, mounted in a specific way.
Locating the Mirror's Zones
We need a practical method for accurately locating any given zone on the mirror for nulling with the tester's knife-edge. Let's look at figure 8d again. This illustration depicts the number three zone (3.53"r) being nulled by our tester's knife edge. This zone divides the mirror into two equal areas, and is by convention referred to as the ".707 zone". How can we be sure that the area being nulled (equally gray all the way around -- the gray "crest" of the bulge) is actually centered on the 3.53"r zone? We will put a specially prepared marker in front of the mirror for locating its zones.
Zonal Masks, or Screens
Zone locating masks for Foucault testing are of two basic types. The traditional type has two equal sized apertures cut into the mask for the left and right side of each zone. Over the years I evolved some major improvements in their design and application that improved their accuracy and convenience in use. Finally, though, I discovered the advantages of the "Everest" style zone locating mask, and began to make and use this type exclusively, rapidly incorporating improvements in Everest's basic concept just as I had with the traditional zone locating masks.
Everest's basic approach was to hang a section of yardstick in front of the mirror being tested with pairs of straight pins protruding from one edge to mark the radii of zones for testing. The straight pins would be seen in sharp silhouette against the zone being nulled -- one could see their outlines, each on either side of the mirror, against the crest of the "doughnut" behind them. As embodied by Everest, the test is somewhat hampered by a perceptual defect. I have noted this defect and have improved the design by making each pair of straight, vertically standing markers (Everest's "pins") into markers curved to the same radii as the zones they represent. The improvement in certainty when locating a zone with this kind of mask is dramatic.
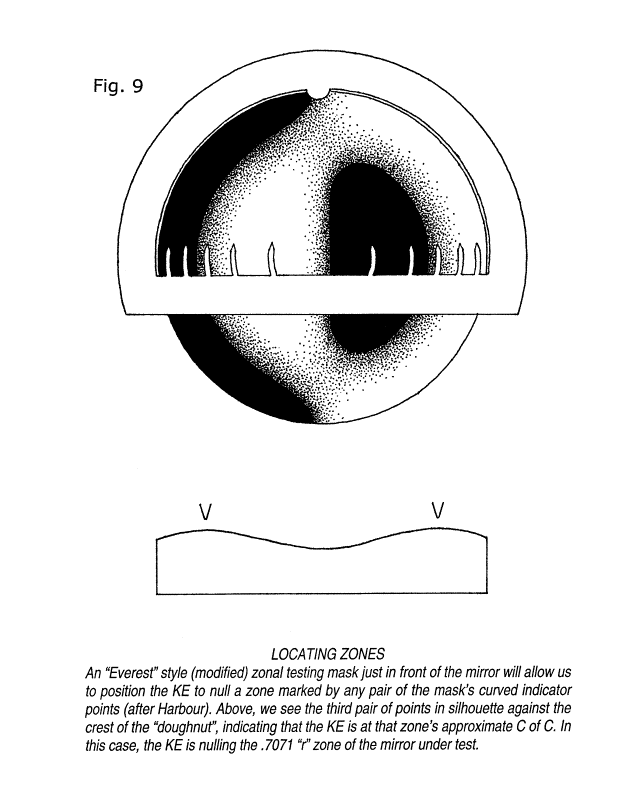
An example of this kind of mask is shown in figure 9. In this particular example (an early form of my improved design) the little marker "horns" protrude up from the crosspiece that supports them. This earlier example has the pointed tips of the indicator horns lying along a meridian across the mirror's horizontal diameter. Horns about twice as long as these, extending equally above and below the mirror's meridian of horizontal diameter, are even better. These curved indicator horns can be made quite long, since they accurately locate a zone lying everywhere underneath each horn's entire length. A curious perceptual effect is at work here. The longer the horns, the more certain the impression of the crest's location underneath them is. When you make your first zone locating masks, make these horns as long as you please, but each of them must be curved along its entire length to the radius of the zone it is intended to mark.
The mask is easily prepared with a beam compass on poster or illustration board, and then cut out with a sharp hobby knife. The configuration shown in figure 9 is just about perfect -- but extend the narrow, curved horns upwards through the mirror's middle, horizontal diameter farther than I show them. I have gotten best results with masks that have the horns extending an equal distance above and below the mirror's horizontal diameter. They should be kept quite narrow, especially for smaller mirrors.
Figure 9 shows the .707r zone being nulled. The middle pair of indicator horns (third pair, outwards from mirror's center) appears to be lying directly atop the crest of the torus-like or doughnut-like bulge. We can have confidence with this indication that the KE is very close to the C of C of this zone. The appearance will be the same for the other zones represented by the other indicator horns when the KE is at their respective centers of curvature. In each case, that zone's particular indicator horns will appear to be lying directly atop the crest of the bulge.
Allowable Errors
As it turns out, figuring the mirror so accurately that the readings for the KE's positions along the optical axis fall precisely as predetermined is neither possible nor necessary. There are two reasons for this. Firstly, there will always be at least a very small domain of ambiguity for the position of the KE when we try to null a zone with the KE on the optical axis. This is because the C of C of any zone being considered, no matter how narrow we define the zone as, does not truly lie on the OA. Secondly, the physical properties of light also decree a range of ambiguity in the location of the plane of focus for any given bundle of rays of light being focused into a point in the focal plane. In fact, no lens or mirror can actually focus light into an infinitesimally small point of light in its focal plane. Rather, when examined up close, we find the tip of the cone of a focused bundle of light not to be a tiny sharp point, but rather a very small disk with a measurable diameter. This little disk of light is the so-called Airy disk (sometimes also referred to as the "diffraction disk").
An image in the focal plane of any mirror or lens is an accumulation of tiny Airy disks all over its surface, representing the tips of many cones of focused light from many different points of origin in the object or field of view being imaged. Each of these myriad cones of focused light is a reflected bundle of parallel light from a single point source in the field of view of the telescope. Each entire bundle of parallel light represents each point source in the field of view and approaches the mirror or lens at a slightly different angle. Each of these bundles of light is then reflected (or transmitted through a lens) at an angle that corresponds to the angle it approached the lens or mirror. Consequently, each bundle of focused light places its Airy disk in a place in the focal plane that corresponds to its point of origin in the field of view. We may think of these little disks as image "pixels", somewhat analogous to the image pixels on the screen of one's computer, although these "pixels" (Airy disks) are circular in shape, unlike the square pixels in a computer screen's image. Or, alternatively, we might think of these Airy disks as analogous to the halftone engraving dots in a newspaper photograph: an accumulation of them all over a plane of focus builds up an image. In our telescope, this plane of Airy disks (the focal plane) might lie on the surface of a piece of ground glass, or on the surface of a photographic plate or piece of photographic film, or on a modern CCD image sensing array, depending on what we are doing with the telescope. Usually, this field of Airy disks is just floating in space in the plane of the field stop of an eyepiece, when we observe visually.
Now, the size of the Airy disks at the tips of each of these bundles of focused rays can be measured, and is different for different sized lenses or mirrors. The size of the Airy disk is a function of the focal ratio of the mirror or lens. If we move slightly inwards along the OA (towards the mirror) from one of these disks in the focal plane for a cone of focused light, we will finally come to a place along the cone where a cross section of it will be a disk having the same diameter as the Airy disk at its tip. Conversely, if we move outwards along the OA (farther away from the mirror or lens) from the Airy disk in the focal plane, we will again come to a point where the re-expanding cone of light has a circular cross section that again equals the diameter of the Airy disk. If we inserted a small square of finely ground glass in the focal plane and moved it back and forth through the focal plane between these two locations we would not see the little focused dot of light on the glass change diameter. In short, it is quite impossible for us to find a precisely defined focal plane for any mirror or lens. Rather, we will have this very short region in which the focus will be found to be acceptable. Thus, we require to figure our mirror only accurately enough that the tip of the cone of light focused by any given zone on the mirror will fall somewhere between these two locations along its optical axis. This range of locations for the C of C of any zone constitutes our allowed (tolerance) error for its location.
Tolerances
The amount of error that is allowed for the location of the focal plane to deviate from its ideal location for any given zone on a mirror has been worked out for us with the science of geometry. For our purposes it is not necessary to elucidate the entire method of determining the allowed error. Rather, we want to know how these allowed amounts of error translate into allowed ranges of location for centers of curvature of any given zone for our mirror. In other words, how large a range of position is allowed for the location of the KE for any given zone under test?
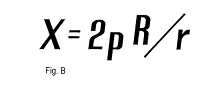
This range of allowed locations for the KE is determined by the simple formula in fig. B. We will call this amount of allowed range of variation in the location of the C of C for any zone "X". This quantity, X, represents the amount of distance the KE may be closer to the mirror by, or farther away from the mirror by, than the computed ideal location of each zone's C of C. We show a summary of the meaning of X in illustration in fig. B(a).
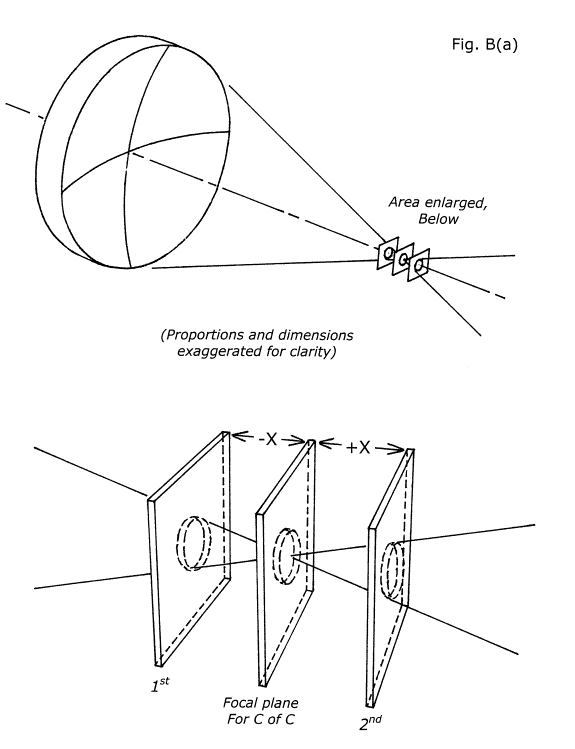
In this diagram we see the cone of light returning from our tester's light source, focusing down to a near point in its focal plane located at its center of curvature. We have inserted a small square of ground glass in this focal plane and note the tiny spot of light representing the Airy disk projected onto it. We may move the ground glass closer to the mirror by the amount "-X", before the cross section of this cone of light represented by the spot projected onto its surface is larger than the Airy disk (position marked "1st"). Also we may move it farther away from the mirror, passing through the focal plane at C of C and advancing beyond it again by a distance equal to "+X", (position marked "2nd") before the cross section of the re-expanding cone of light is again as large as the Airy disk.
For the other terms of the formula, "p" is the radius of the Airy disk at the mirror's focus for infinity, "R" is again the radius of curvature of the mirror and "r" is again the radius of the zone on the mirror under test. To find "p", the radius of the Airy disk for any mirror at its focus, we will use the expression in fig. D, where "F" is the focal length, and "D" is the diameter of the mirror, and "w" is the wavelength of yellow-green light (.0000216") that has by convention been adopted as the standard for these purposes.
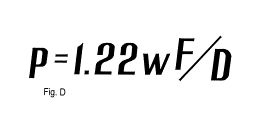
After determining the radius of the Airy disk for our mirror, we can plug it into the formula as in fig. B and determine X, the allowed variation of location of C of C for any zone. Now, we've already computed "d" for the five zones whose centers of curvature we wish to command into their predetermined locations on the OA through figuring. For each value of "d" for each zone, we add "X" to and subtract "X" from. Any reading for the location of the C of C for any zone that falls between these computed values is acceptable -- with a certain caveat that we shall shortly stipulate.
Interpreting Test Results
Figuring our mirror so that the centers of curvature of each zone as measured with the KE fall within tolerances will give us an acceptable mirror. However, using a graph to visualize the relationships of the plot of each KE setting with each other KE setting will help us to visualize and plan the best approach to refine and idealize the mirror's figure.
A graph of the values of "d", and "X", and the actual locations of C of C for each zone as measured with the KE is easy to construct. We show such a graph to help manage testing and figuring in figure C. The vertical line on the left side of the graph has index marks in hundredths of an inch.
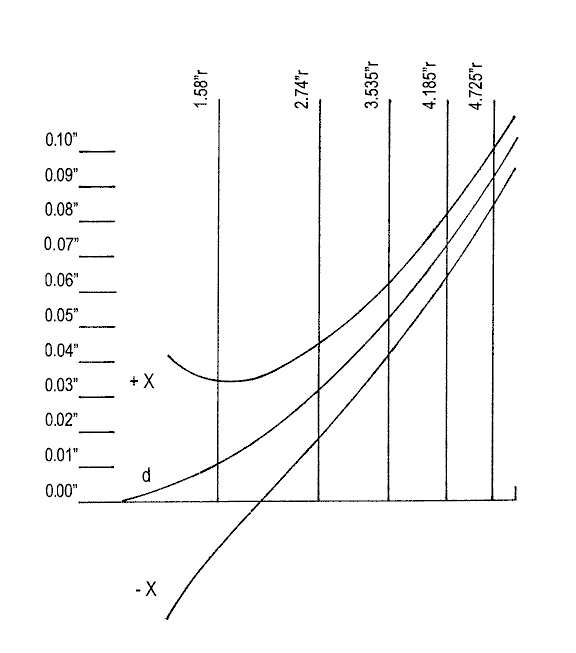
The horizontal line at the bottom of the graph represents the mirror from its center outwards, radius-wise; the vertical lines extending up from this line represent the locations of the five zones, radius-wise from the center of the mirror that we will test for. The horn shaped figure sweeping upwards to the right and away from the center of the mirror represents the envelope or domain of allowed readings of the KE for the centers of curvature of any zone on the mirror under test. The middle curved line (inside the "horn") is for the pre-computed plots for "d" for any zone on the mirror (location of C of C relative to C of C for center of mirror). The upper curved line of the tolerance horn represents the allowed range of positions for "d" that are farther away from the mirror than the ideal positions. The bottom curved line of the tolerance horn represents the allowed range of positions for "d" that are closer to the mirror than the ideal positions. In order to plot relatively smooth and accurate lines for the values of "d" and "X", it is helpful to compute them for zones with radii in half inch increments for the mirror, even though we will be testing for only the five zones previously computed for.
Metric ruled graph paper is convenient for making these test result graphs, as the centimeter markings are a convenient size to represent hundredths of an inch, and they are subdivided into ten smaller units (millimeters) to help one represent thousandths of an inch. Use these to represent the vertical ordinate, for plotting the relative locations of the KE settings. For the horizontal, radius-wise ordinate extending to the right, use a ruler. An inexpensive machinist's ruler divided in tenths and hundredths of an inch is handy for this purpose.
Quick Summary: Procedure and Analysis
You now have everything you need to know to accurately test and plot your test results for the mirror you are figuring. To get everything concisely and compactly in mind, we will now summarize the test procedure and management of test data.
Set the "Y" axis stage of your tester to its zero setting, and carefully locate it along the mirror's optical axis to null its very central region. With your pre-cut zone testing mask in front of the mirror, back the Y-axis stage carrying the KE away from the mirror to find the C of C of the first zone and note its location as indicated by the micrometer (write it down). Then, back the KE up again until the next zone as indicated by the horns on the mask is nulled and note, again, your micrometer's reading. Next, repeat the procedure for the third zone out from the center, the fourth, and finally the fifth, recording the location of each one's C of C as indicated by the micrometer. You will find during testing that unless the Y-axis stage runs truly along the mirror's OA you will have to manipulate the lateral, X-axis movement, to make a good null each time. This is okay.
Plot your recorded locations of each zone's C of C on your previously prepared graph for this purpose in their correct locations, and then connect these plots with lines as shown in our example in fig. E.
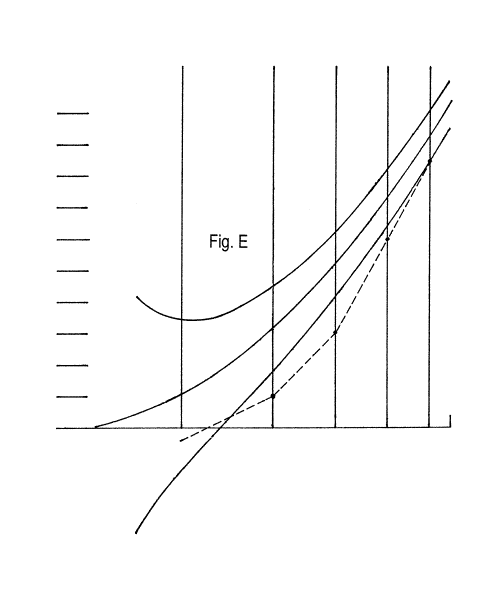
Of course, at the beginning of figuring, the line of the KE settings will probably be "all over the place", not even approximately fitting inside the tolerance horn of the graph. But, you might get a pleasant surprise: you might be "in the ballpark" from the start. I knew a gentleman who "accidentally" figured his mirror into a good paraboloid just by polishing it out! (Don't expect this). Let's consider fig. E as a representative example of typical KE settings for one test run somewhere near the end of the figuring process. Note that the first reading of the KE for the first zone is actually closer to the mirror than the C of C of its central region. I.e., we had to advance the KE towards the mirror to find it, rather than find it pleasantly located in its proper location a tiny ways away from the C of C of the central region. The plots for the second, third, and fourth zone fall outside the tolerance horn. But note that the overall shape of the connected plots approximates the shape of the tolerance horn, envelope.
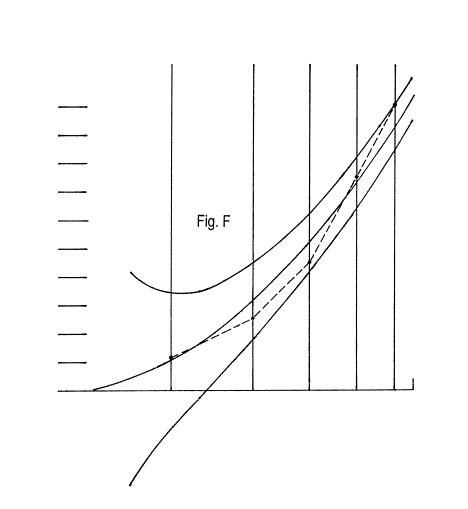
In fig. F we have relocated all of the plots farther up on the graph by an equal amount, each of them, until they all fit inside the tolerance envelope. This is allowed: it is merely the equivalent of starting with the tester located closer to the mirror by that amount of distance.
Now the plots of all centers of curvature are lying everywhere inside of the tolerance envelope. Our ten-inch mirror of sixty inches focal length (focal ratio of six to one, or "f/6") is now well enough figured that it will show no spherical aberration in use. Even if the tips of the cones of focused bundles of light from any zone on the mirror come to a focus into a plane farther away from their ideally computed ones, the blur circles representing the cross sections of these cones of light where they intersect their planes of ideal focus and pass through them will be no larger than their Airy disks at true focus would be in their ideal focal planes.
The tolerances as computed by the formulae given are considered "loose" by most authorities; that is to say, they are considered to be the least demanding for acceptable performance for a telescope's objective mirror, and many authorities recommend making a mirror's curve to at least twice as demanding tolerances. By all means, one may continue figuring until his or her mirror's plots of KE settings fall very close to the middle curve of the graph (for values of "d").
I have tested many mirrors on the stars whose plots were spread out for the full tolerance envelope allowed by the graph. On nights of extremely steady air and at magnifications approaching 50X per inch (for larger mirrors) none of them ever showed any detectable halo of spherical aberration. However, the caveat we promised to convey to you in this regard (using up all the available space inside the tolerance horn) we should now specify. The connected line of plots for KE positions should not be wildly irregular, but rather deviate in a rather smooth, consistent fashion as with the example in figures E and F.
Please note that I have never defined the allowable tolerances for the disparity of focal planes for different zones of a mirror in terms of fractions of wavelengths of light. Instead, I have defined them in far more unequivocal terms, terms that lead one to an intuitive understanding of what tolerances mean. Simple geometry, algebra, and extensive practical verification have unequivocally validated these procedures for me.
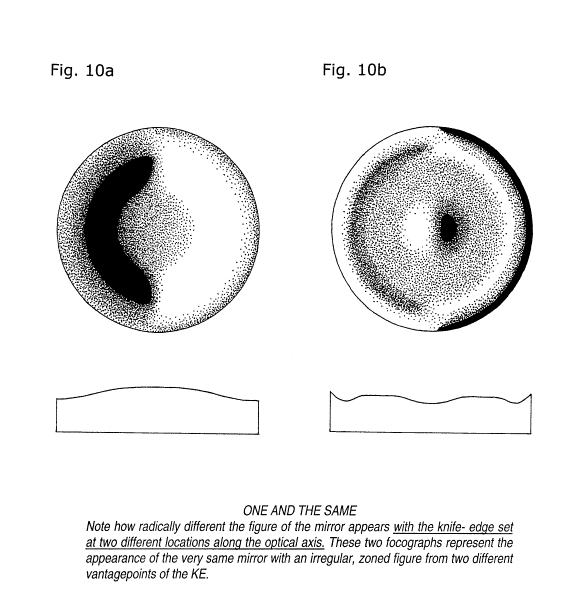
Before leaving our introduction to Foucault testing, it will be interesting to survey a mirror with the knife-edge whose figure is very irregular. fig. 10(a) and 10(b) show the same mirror (actual mirror from my extensive files) from two different vantage points along its OA for the KE. Note how radically different this mirror looks with the KE located in widely disparate positions along the OA.
I have kept this treatment of Foucault testing to the very barest essentials. A much more exhaustive treatment is possible; however, a well explained introduction to the subject for beginners is what has been most wanted.
Other titles to help the beginning amateur telescope maker will shortly be in preparation. The very next help article will be a well illustrated description with complete instructions for building a very capable "over and under" type Foucault tester. In the article I will show how to build a high precision measuring engine (the tester) with little or only minimal machining.
Later I will be preparing articles on subjects for the ATM for which well written and well illustrated how-to literature seems to be scarce. These topics will be comprehensively and exhaustively treated, and will include articles on the construction of large channeled ceramic grinding tools, sub-diameter grinding, polishing, and figuring techniques for working large mirrors, and quick and painless polishing tools for large and small mirrors.
The above article is Copyright © 2001 David Anthony Harbour. It is reporoduced here with his full permission (and at his personal urging). This reproduction of "Understanding Foucault" is only one portion of the excellent writings David has penned dealing with Foucault Testing and mirror making. More of his clear, down to earth, information and work methods is available in the book "Understanding Foucault" available through Amazon.com. I encourage readers to get the book with the expanded information including figuring a mirror, test procedures, and details of his tester designs.